What is attosecond transient absorption spectroscopy (ATAS)?
Attosecond transient absorption spectroscopy (ATAS) is an ideal technique to probe electronic dynamics, since it analyzes the light pulse after it has interacted with the electronic state of the system. ATAS measured specifically the transmitted light of the pulse. Using the initial spectrum of the pulse (before interaction) as a reference, allows one to calculate the absorption spectrum of the system, i.e., how many photons with a specific energy where absorbed by the system. Such an absorption spectrum contains information about the electronic state in the form that it reveals where energetically the excited states of the system (that can be accessed by one-photon transition) lie. Therefore, absorption spectra have been of high interest since the very beginning of quantum mechanics. At the time, it was the primary way for researchers to probe atomic systems. Also now-a-days, absorption spectroscopy is still one of the mostly used technique for studying electronic structure and, in particular, the role of many-body effects [1].
Along with technology and shorter and shorter pulses, absorption spectroscopy moved into the time domain and became more and more a way to probe electronic dynamics as well. With ATAS absorption spectroscopy has entered the attosecond time scale, which is the characteristic time scale of electrons in atoms and molecules [corresponding to excitation energies of several electronvolts (eVs)].
Using attosecond (as) pulses for transient absorption spectroscopy brings along two advantages. On the one side, the time resolution moves obviously into the attosecond regime, and, on the other side, the spectral range electronic states that can be probed increases with attosecond pulses and is now with several eVs much larger than with femtosecond (fs) and picosecond (ps) pulses (sub-eV and sub-meV spectral width). In other words, ATAS can probe the ultrafast electronic motion of several electronic states at the same time.
Probing ionization dynamics with ATAS
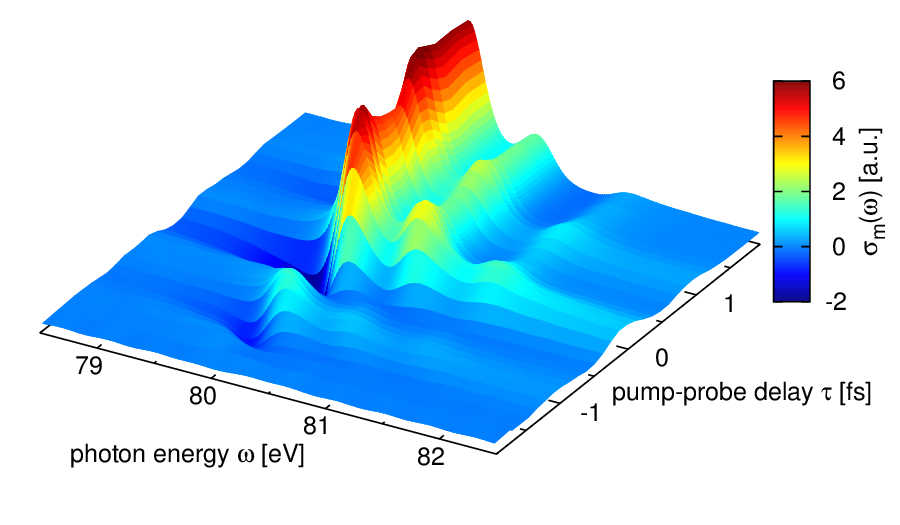
Figure 1: Transient absorption spectrum of atomic krypton as it gets ionized. The 3 transition lines correspond to the three resonant excitations that probe the krypton ion. Illustration is taken from Ref. [2]. © 2012 American Physical Society.
Recently, I studied how ATAS can be used to learn more about the sub-cycle dynamics of tunnel ionization [2]. Tunnel ionization is viewed as a process where the electric field of the ionizing pulse is comparable with the inner-atomic Coulomb forces such that the effective one-particle potential of the electron is highly distorted. The distortion is, however, not as severe that the electron could just escape the nucleus because there is a potential barrier that the electron cannot overcome—at least in a classical picture. Quantum-mechanically, the electron can escape in this situation via tunneling a pure quantum phenomenon, where the electron passes through a region in space that is classically forbidden because of energy arguments (for more infos please see Chapter 3 of my PhD thesis or Ref. [3]).
In an collaboration [4] with the experimental group of Dr. Goulielmakis (from the Max-Planck-Institut für Quantumoptik) we studied the behavior of the hole populations and measured also phases of each ionic state (for more informations on this work please click here). In Ref. [2], the focus lies more on the detailed understanding of the dynamics of the phases of each ionic state. In both studies, we studied the concrete example of tunnel ionization of krypton atoms such that Kr\(^+\) ions are generated with an electron missing in one of the \(4p\)-orbitals. Since we consider spin-orbit coupling, the orbitals are \(4p_j^m\), where \(j=\frac{1}{2},\frac{3}{2}\) is the total angular momentum and \(m=-j,…,j\) its projection on the laser polarization axis. The corresponding ionic states \([4p_{j}^{m}]^{-1}\) are \([4p_{1/2}^{1/2}]^{-1}\), \([4p_{3/2}^{1/2}]^{-1}\), and \([4p_{3/2}^{3/2}]^{-1}\), where the sign of \(m\) are ignored since both states behave exactly the same.
The attosecond probe pulse, which is used for ATAS, probes these ionic states by a resonant excitation of an \(3d\)-electron into the \(4p\)-vacancy. Overall there are three energetically-distinct excitations:
- \([4p_{1/2}^{m}]^{-1} \rightarrow [3d_{3/2}^{m}]^{-1}\),
- \([4p_{3/2}^{m}]^{-1} \rightarrow [3d_{3/2}^{m}]^{-1}\),
- \([4p_{3/2}^{m}]^{-1} \rightarrow [3d_{5/2}^{m}]^{-1}\).
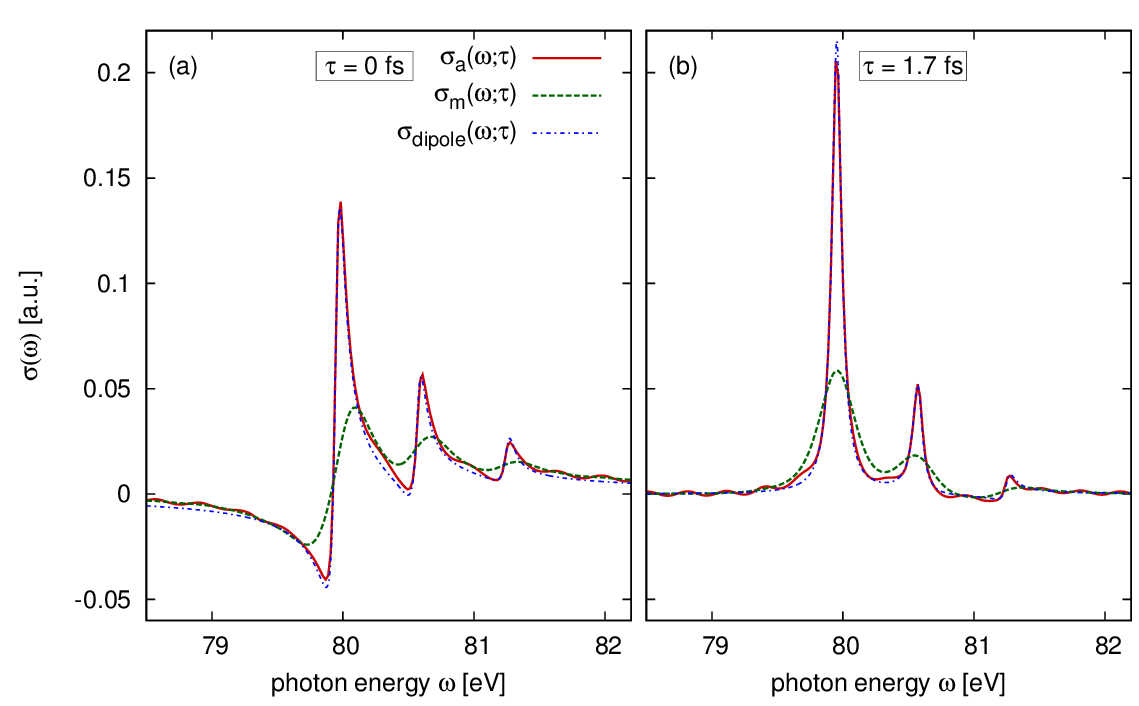
Figure 2: Transient absorption spectrum of atomic krypton for two specific pump-probe delays \(\tau=0~\textrm{fs}\) and \(1.7~\textrm{fs}\). The strong line deformations during the pump pules (\(\tau=0~\)fs) indicate large quantum phase shifts in the \([4p_{j}^{m}]^{-1}\) ionic states. Illustration is taken from Ref. [2]. © 2012 American Physical Society.
These three excitations lead three absorption lines, which are shown in Fig. 1 for a situation where the Kr gets tunnel ionized by a strong-field IR pulse. In addition to the energy axis which refers to the energy of the photon there is a time delay axis showing the pump-probe delay between the strong-field pump pulse and the attosecond probe pulse. A negative pump-probe delay means the probe pulse comes first and probes the atom before the tunnel ionization, and positive delays mean the pump pulse comes first and the probe pulse measures the tunnel-ionized atom. Please keep in mind that the attosecond pulse is with 240 as much shorter than the strong-field pulse, which has a duration of 2 fs. Therefore, the attosecond probe pulse takes at each delay a snapshot of the dynamics. In Fig. 2, two such snapshots for the pump-probe delay of 0 fs and 1.7 fs are shown. By varying this delay continuously the entire ionization dynamics can be recorded.
Seeing ultrafast quantum phase dynamics
What is very interesting, the shapes of the absorption lines in Fig. 1 vary quite strongly for pump-probe delay between -1 fs and 1 fs. The height of the lines are related to the hole populations in the \(4p\) orbitals and the line shapes are related to the phases of each ionic states. Here, we are interested in the phase dynamics and what mechanism causes the phases to change so rapidly. The exact values of the phases can be extracted by fitting an oscillating dipole model to the data shown in Fig. 1. The red line in Fig. 3 shows the phase as a function of pump-probe delay for the \([4p_{3/2}^{m}]^{-1}\) ionic state (main transition line in Figs. 1 and 2). Within 2 fs the phase changes by more than \(2\pi\).
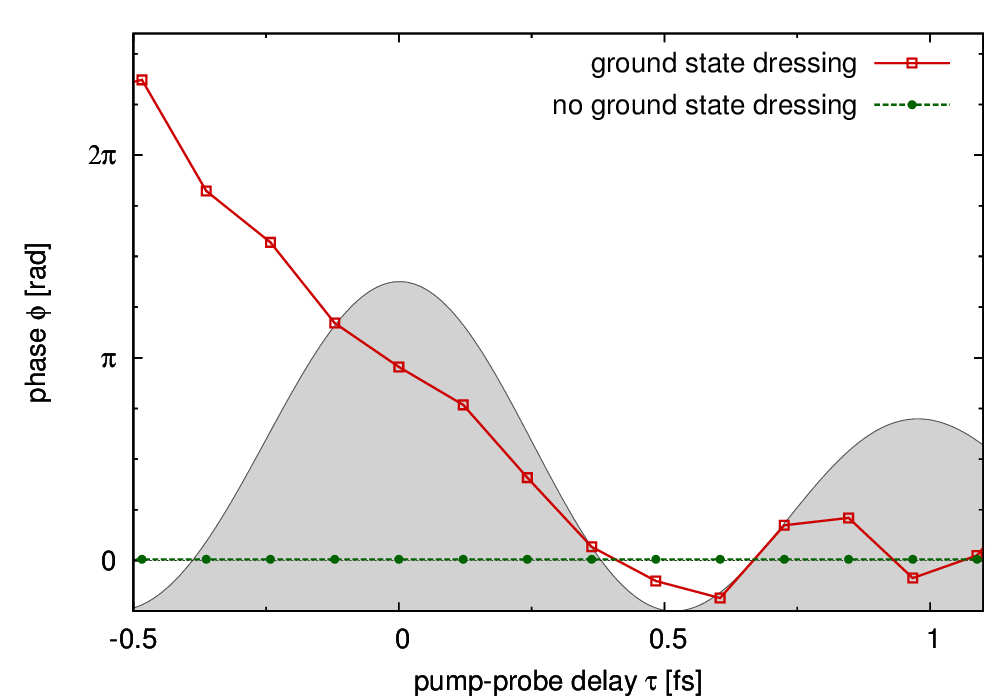
Figure 3: Phase dynamics of the \([4p_{3/2}^{m}]^{-1}\) ionic states. The red (green) curve shows the phase dynamics with (without) strong-field coupling between ion and ionized electron. Illustration is taken from Ref. [2]. © 2012 American Physical Society.
After a detailed analysis, we found that the strong electric field of the pump IR pulse couples the \(4p\)-ionic hole with the tunnel-ionized electron and, therefore, influences the ionic hole phase dramatically. If we switch this interaction off, we find that this phase dynamics disappears and stays constant throughout the entire tunnel ionization process (green curve in Fig. 3).* What I have not said so far is that it is only possible to measure relative phases. The phase of \([4p_{3/2}^{m}]^{-1}\) shown in Fig. 3 is measured relative to the phase of \([3d_{5/2}^{m}]^{-1}\). Especially important is that the strong-field coupling of the hole with the excited electron does not exist for \(3d\) holes because the ionization potential is so high (x7 larger than for \(4p\)) that even the large electric field of the pump pulse cannot couple them. Therefore, the phase dynamics of \([3d_{5/2}^{m}]^{-1}\) is easily understood and can be used as a reference.
Summary & outlook
With this study, we could nicely show how ATAS can be used to learn not just something about populations but also about quantum phases of ionic states. Knowing the phases and the absolute values of each quantum state allows us to recover the entire electronic dynamics. Combined with the high control of the pump-probe delay, the complete electronic dynamics can be probed on an attosecond time scale.
*The field-driven coupling between the hole and the excited electron is only turned-off after the probe pulse because before the probe pulse the very same term is need to tunnel ionize the atom. Therefore, in reality this terms can never be turned off.
References:
[1] D. Krebs, S. Pabst, and R. Santra, Am. J. Phys., accepted.
[2] S. Pabst et al., Phys. Rev. A 86, 063411 (2012); [pdf].
[3] S. Pabst, Eur. Phys. J. Spec. Top. 221, 1 (2013).
[4] A. Wirth et al., Science 334, 195 (2011).
[5] L. Greenman et al., Phys. Rev. A 82, 023406 (2010); [pdf].